向量(vector):在游戏中通常表示位置,移位,方向,速度和作用力(请看directx数学基础1)矩阵(matrix):在游戏中提供高效的变换方式,几何变换与坐标变换
矩阵(矩形实数数组)
矩阵乘法(a中的行向量的维数必须与b中的列向量的维数相同)
例如: 
转置矩阵(transpose: 对一个矩阵的行和列进行互换)
标记为T
单位矩阵(identity: 除了对角线上的元素为1外,其他元素均为0)
单位矩阵相当于1 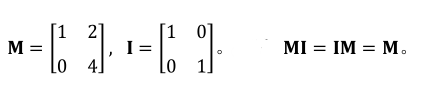
逆矩阵(inverse: 乘法的逆运算(矩阵除法运算))
性质: 
基本变换(4x4矩阵与向量-矩阵乘积来描述变换)
齐次坐标(homogeneous coordinate): 用于表示3D向量或点的四元组
通过它的第4个坐标分量w(控制平移)来判断:
缩放: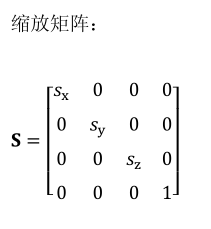

例子:
假设我们通过一个最小点(−4,−4,0)和一个最大点(4,4,0)来定义一个正方形,我们希望
将正方形沿 x 轴缩小 0.5 倍,沿 y 轴放大 2.0 倍,z 轴保持不变则对应的缩放矩阵为: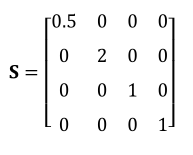
再对正方形进行缩放(变换),将正方形的两个点与该矩阵相乘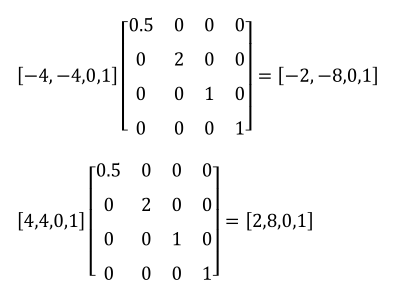
结果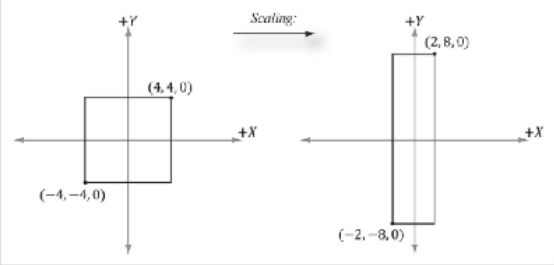
旋转:
绕n(x,y,z)轴旋转的’万能’旋转矩阵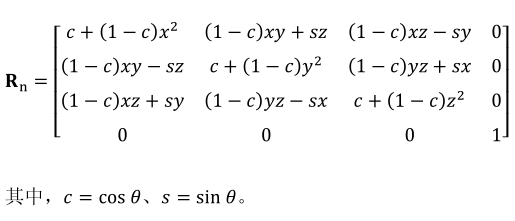
正交矩阵(orthogonal matrix): 行向量都是相互垂直且为单位长度性质:
它的逆矩阵与它的转置矩阵相等 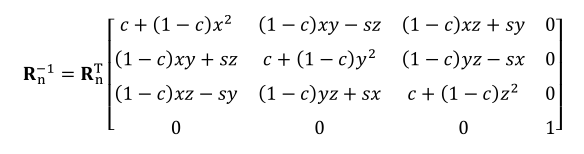
绕x,y,z轴(n=(1,0,0) n=(0,1,0) n=(0,0,1))旋转的矩阵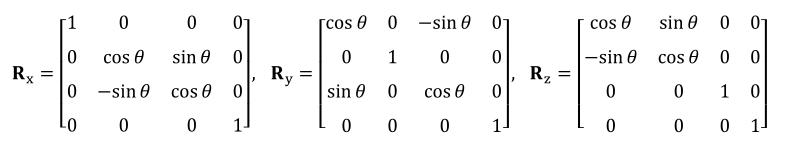
例子:
假设我们通过一个最小点(−1,0,−1)和一个最大点(1,0,1)来定义一个正方形。让正方形
绕着 y 轴的顺时针方向旋转−30º(即,逆时针方向旋转 30º)。则y轴旋转矩阵为: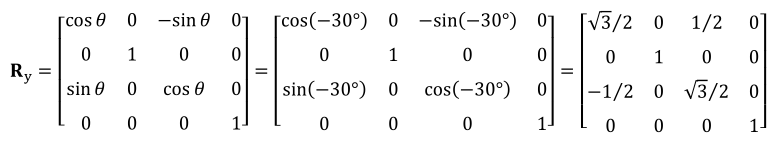
再对正方形进行旋转(变换),将正方形的两个点与该矩阵相乘:
结果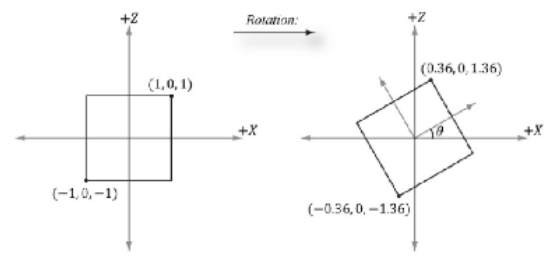
平移:
平移矩阵的逆矩阵如下: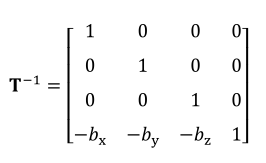
例子:
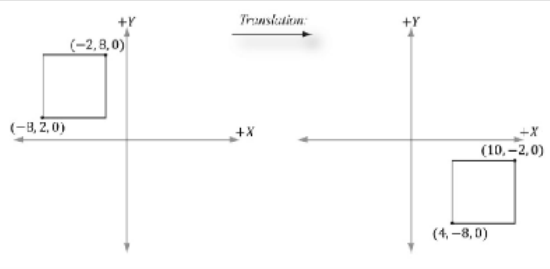
假设我们通过一个最小点(−8,2,0)和一个最大点(−2,8,0)来定义一个正方形。让正方形
沿x轴平移12,沿y轴平移−10,z轴保持不变。则对应的平移矩阵如下: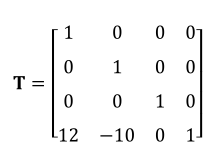
再对正方形进行平移(变换),将正方形的两个点与该矩阵相乘:
结果